Event segment

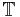A segment or trajectory is a relation between an element of an arbitrary set $Z$ and a time of time base $\mathbb{T}$ [Zeigler76] and [ZPK00]. As timed sequences of events, event segments are a special class of the general segment. Event segments are used to define Timed Event Systems such as DEVS, timed automata, and timed petri nets.

1 Event segments
2 Timed language
3 References

Event segments

Event and null event

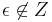An event is a label that abstracts a change. Given an event set $Z$ , the null event denoted by $\epsilon \not \in Z$ stands for nothing change.

Time base

The time base of the concerning systems is denoted by 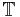$\mathbb{T}$ , and defined

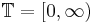
$\mathbb{T}=[0,\infty)$

as the set of non-negative real numbers.

Timed event

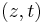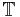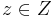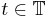A timed event $(z,t)$ over an event set $Z$ and the time base $\mathbb{T}$ denotes that an event $z \in Z$ occurs at time $t \in \mathbb{T}$ .

Null event segment

The null event segment over time interval $[t_l, t_u] \subset \mathbb{T}$ is denoted by $\epsilon_{[t_l, t_u]}$ which means that there is no event over $[t_l, t_u]$ .

Unit event segment

A unit event segment is either a null event segment or a timed event.

Concatenation

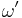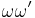Given an event set $Z$ , concatenation of two unit event segments $\omega$ over $[t_1, t_2]$ and $\omega'$ over $[t_3, t_4]$ is denoted by $\omega\omega'$ whose time interval is $[t_1, t_4]$ , and implies $t_2 = t_3$ .

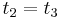Multi-event segment

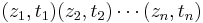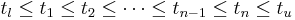A multi-event segment $(z_1,t_1)(z_2,t_2) \cdots (z_n,t_n)$ over an event set $Z$ and a time interval $[t_l, t_u] \subset \mathbb{T}$ is concatenation of unit event segments $\epsilon_{[t_l,t_1]},(z_1,t_1), \epsilon_{[t_1,t_2]},(z_2,t_2),\ldots, (z_n,t_n),$ and $\epsilon_{[t_n,t_u]}$ where $t_l\le t_1 \le t_2 \le \cdots \le t_{n-1} \le t_n \le t_u$ .

Timed language

The universal timed language over an event set $Z$ and a time interval $[t_l, t_u] \subset \mathbb{T}$ , is denoted by $\Omega_{Z,[t_l, t_u]}$ , and is defined as the set of all possible event segments. Formally,

$\Omega_{Z,[t_l,t_u]}=\{(z,t)^*| z \in Z \cup \{\epsilon\}, t \in [t_l, t_u] \}$

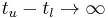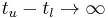where $^*$ denotes a none or multiple concatenation(s) of timed events. Notice that the number of events in an event segment $\omega \in \Omega_{Z,[t_l, t_u]}$ can be one of zero, finite or infinite. Infinitely many events in an event segment $\omega \in \Omega_{Z,[t_l, t_u]}$ implies that $t_u - t_l \rightarrow \infty$ , however $t_u - t_l \rightarrow \infty$ does not imply infinite many events in it.

A timed language over an event set $Z$ and a timed interval $[t_l, t_u]$ is a set of event segments over $Z$ and $[t_l, t_u]$ . If $L$ is a language over $Z$ and $[t_l, t_u]$ , then $L \subseteq \Omega_{Z, [t_l, t_u]}$ .

References

[Zeigler76] Bernard Zeigler (1976). Theory of Modeling and Simulation (first ed.). Wiley Interscience, New York.
[ZKP00] Bernard Zeigler, Tag Gon Kim, Herbert Praehofer (2000). Theory of Modeling and Simulation (second ed.). Academic Press, New York. ISBN 978-0127784557.